图的部分基础概念

完全图边数

1. 无向图

对于无向图 $G = (V, E)$，若任意两个顶点之间都有一条边相连，这种图被称为完全图。

边的数量推导

图中有 $|V|$ 个顶点。
任意两个顶点之间都有一条边相连，选两个顶点的方法总共有：
$$
\binom{|V|}{2} = \frac{|V|(|V|-1)}{2}
$$
因此，完全图的边数为：
$$
|E| = \frac{|V|(|V|-1)}{2}
$$
当且仅当边数达到这个值时，说明每一对顶点之间都有边相连，图才是完全图。

举例

假设图中有 4 个顶点 {A, B, C, D} ，选两个顶点的所有可能方法为：

(A, B), (A, C), (A, D)
(B, C), (B, D)
(C, D)

这些组合一共 6 种，数量可以用组合公式计算：
$$
C^{|V|}_2 = \frac{|V|(|V|-1)}{2}
$$

2. 有向图

对于有向图 $G = (V, E)$，若任意两个顶点之间都有一条方向不同的有向边（即 $u \to v$ 和 $v \to u$），这种图被称为完全有向图。

边的数量推导

图中有 $|V|$ 个顶点。
对于任意两个顶点 $u$ 和 $v$：
- $u \to v$ 是一条有向边。
- $v \to u$ 是另一条有向边。
每一对顶点之间都有两条方向相反的有向边，且顶点对的总数为 $|V|(|V|-1)$（排列方式，顺序不同的对算作不同）。
因此，完全有向图的边数为：
$$
|E| = |V|(|V|-1)
$$

当且仅当边数达到这个值时，说明任意两点之间都有方向不同的有向边，图才是完全有向图。

举例

假设图中有 4 个顶点 {A, B, C, D} ，从中选两个顶点并赋予方向，所有可能的方法为：

从 A 指向 B ： (A, B)
从 B 指向 A ： (B, A)

对于每一对顶点，都会生成两个有向边。因此，从 |V| 个顶点中挑选两个顶点并考虑方向的总数为排列公式：
$$
A^{|V|}_2 = |V| \cdot (|V|-1)
$$

总结

无向图：完全图的边数为 $|E| = \frac{|V|(|V|-1)}{2}$。
有向图：完全有向图的边数为 $|E| = |V|(|V|-1)$。

原因在于组合（无向图）与排列（有向图）的不同。

图的存储

邻接矩阵

https://www.lddgo.net/chart/character-relationship

定义

邻接矩阵（Adjacency Matrix）是表示图（无向图或有向图）的一种常用方式，使用一个矩阵来描述顶点与顶点之间的连接关系。

给定一个图 $G = (V, E)$，其中 $|V| = n$（顶点数为 $n$），邻接矩阵是一个 $n \times n$ 的方阵 $A$。
矩阵中的每个元素 $A[i][j]$ 表示从顶点 $i$ 到顶点 $j$ 是否有边存在：
- 无向图：若顶点 $i$ 和 $j$ 之间有边，则 $A[i][j] = 1$（或权值）；否则 $A[i][j] = 0$。
- 有向图：若存在从顶点 $i$ 指向顶点 $j$ 的边，则 $A[i][j] = 1$（或权值）；否则 $A[i][j] = 0$。

邻接矩阵的构造

1. 无权图

无向图：$A[i][j] = 1$ 表示顶点 $i$ 和 $j$ 之间有边。
有向图：$A[i][j] = 1$ 表示存在从顶点 $i$ 指向顶点 $j$ 的有向边。

2. 带权图

无向图：$A[i][j]$ 存储顶点 $i$ 和 $j$ 之间的权值。
有向图：$A[i][j]$ 存储从顶点 $i$ 到顶点 $j$ 的权值。
若无边连接，则 $A[i][j] = 0$ 或 $A[i][j] = \infty$（表示不可达）。

邻接矩阵的例子

1. 无向无权图

假设有 4 个顶点 $V = {A, B, C, D}$，边集 $E = {(A, B), (B, C), (C, D)}$。

邻接矩阵如下：
$$
A =
\begin{bmatrix}
0 & 1 & 0 & 0 \
1 & 0 & 1 & 0 \
0 & 1 & 0 & 1 \
0 & 0 & 1 & 0
\end{bmatrix}
$$

$A[1][2] = 1$ 表示顶点 $A$ 和 $B$ 相连。
矩阵是对称的，因为这是一个无向图。

2. 有向图

假设有 4 个顶点 $V = {A, B, C, D}$，边集 $E = {(A, B), (B, C), (C, A)}$。

邻接矩阵如下：
$$
A =
\begin{bmatrix}
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
1 & 0 & 0 & 0 \
0 & 0 & 0 & 0
\end{bmatrix}
$$

$A[1][2] = 1$ 表示存在从 $A$ 到 $B$ 的边。
$A[3][1] = 1$ 表示存在从 $C$ 到 $A$ 的边。
矩阵不对称，因为边是有方向的。

邻接矩阵的特点

优点

表示清晰，适合进行快速查询：判断两顶点是否相连只需 $O(1)$ 时间。
易于实现图相关的算法，例如求最短路径或最小生成树。

缺点

空间复杂度高：需要 $O(n^2)$ 的存储空间，即使是稀疏图（边较少的图）。
不适合稀疏图：对于顶点很多但边很少的图，邻接矩阵会浪费大量空间。

邻接矩阵的应用

图的遍历：如深度优先搜索（DFS）和广度优先搜索（BFS）。
图的算法：如 Floyd-Warshall 算法、Dijkstra 算法等求最短路径问题。
快速判断顶点连接性：通过矩阵快速判断顶点间是否有边。

邻接矩阵是一种常用的图表示方式，但对于稀疏图，更适合使用邻接表来节省空间。

邻接表

定义

邻接表（Adjacency List）是一种表示图（无向图或有向图）的常用方式，用于描述顶点与顶点之间的连接关系。
邻接表通过为每个顶点维护一个链表（或数组）来存储与之相连的其他顶点信息。

给定一个图 $G = (V, E)$，其中 $|V| = n$（顶点数为 $n$）。
邻接表使用一个大小为 $n$ 的数组，其中每个元素对应一个顶点，其值为与该顶点相邻的顶点集合。

邻接表的处理方法是这样的。

1、图中顶点用一个一维数组存储，另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。

2、图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图称为顶点vi作为弧尾的出边表。

邻接表的构造

1. 无权图

无向图：若顶点 $i$ 和顶点 $j$ 之间有边，则将 $j$ 加入顶点 $i$ 的邻接链表中，同时将 $i$ 加入顶点 $j$ 的邻接链表中。
有向图：若存在从顶点 $i$ 指向顶点 $j$ 的边，则将 $j$ 加入顶点 $i$ 的邻接链表中。

2. 带权图

无向图：每个链表节点存储一个二元组 $(j, w)$，其中 $j$ 为相邻顶点，$w$ 为权值。
有向图：每个链表节点存储一个二元组 $(j, w)$，表示从顶点 $i$ 指向顶点 $j$ 的边权值为 $w$。

邻接表的例子

1. 无向无权图

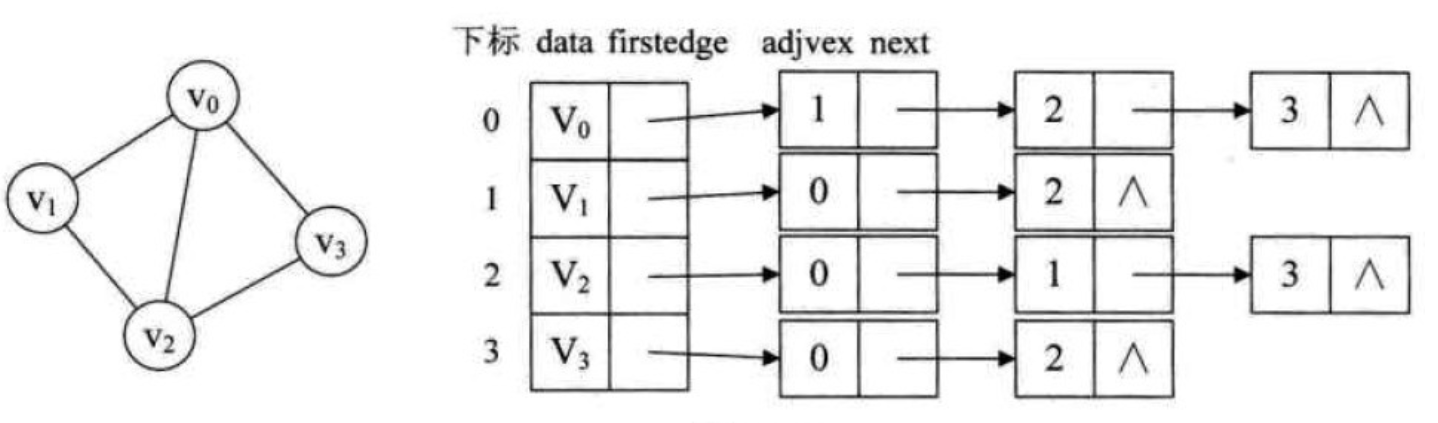
2. 有向无权图

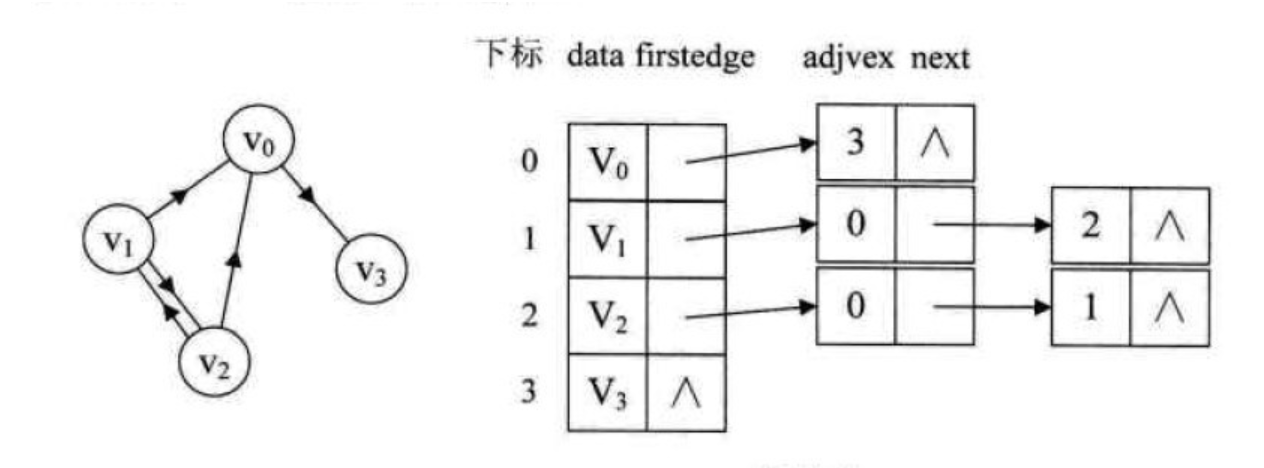
3. 带权图

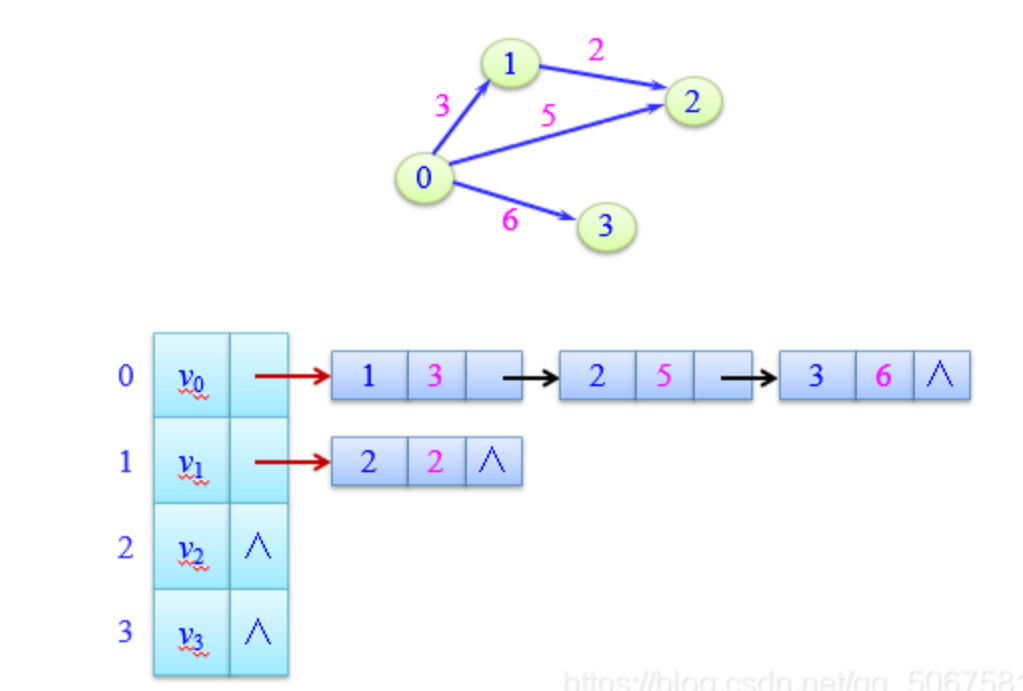
邻接表的特点

优点

节省空间：邻接表的存储复杂度为 $O(V + E)$，对于稀疏图（边较少的图）非常高效。
灵活性高：添加或删除边操作简单，适合动态图的操作。

缺点

查询效率较低：判断两顶点是否相连需要遍历链表，时间复杂度为 $O(\text{链表长度})$。
不适合密集图：对于边较多的图，邻接表会增加复杂度。

邻接表的应用

图的遍历：如深度优先搜索（DFS）和广度优先搜索（BFS）。
动态图的处理：如频繁插入或删除边的场景。
稀疏图的存储：在顶点数远大于边数时，邻接表是更高效的存储方式。

邻接表与邻接矩阵的比较

特性	邻接矩阵	邻接表
空间复杂度	$O(V^2)$	$O(V + E)$
查询效率	$O(1)$	$O(\text{链表长度})$
插入效率	$O(1)$（修改矩阵）	$O(1)$（修改链表）
适用场景	密集图	稀疏图